RESOLUÇÃO-RE Nº 898, DE 29 DE MAIO DE 2003

O Adjunto da Diretoria Colegiada da Agência Nacional de Vigilância Sanitária, no uso da atribuição, que lhe confere a Portaria n.º 238, de 31 de março de 2003,

considerando o disposto no art.111, inciso II, alínea "a" § 3º do Regimento Interno aprovado pela Portaria nº 593, de 25 de agosto de 2000, republicada no DOU de 22 de dezembro de 2000,

considerando que a matéria foi submetida à apreciação da Diretoria Colegiada, que a aprovou em reunião realizada em 6 de março de 2003, resolve:

Art. 1º Determinar a publicação do "Guia para planejamento e realização da etapa estatística de estudos de biodisponiblidade relativa/bioequivalência" anexo.

Art. 2º Fica revogada a Resolução RE no 484, de 19 de março de 2002.

Art. 3º Esta Resolução entra em vigor na data de sua publicação.

DAVI RUMEL

ANEXO

GUIA PARA PLANEJAMENTO E REALIZAÇÃO DA ETAPA ESTATÍSTICA DE ESTUDOS DE BIODISPONIBLIDADE RELATIVA/BIOEQUIVALÊNCIA

1. Introdução

O objetivo deste guia é fornecer algumas recomendações gerais para análise estatística nos estudos de biodisponiblidade relativa/bioequivalência.

2. Planejamento Um dos critérios para escolher um delineamento apropriado é verificar se o delineamento selecionado pode identificar e isolar a variabilidade inter-individual na análise de dados. Qualquer delineamento que venha remover essa variação da comparação entre formulações pode ser apropriado.

O planejamento experimental mais utilizado nos ensaios de biodisponibilidade relativa/ bioequivalência é o cruzado (crosssover), cujos detalhes serão discutidos nesse guia.

2.1 Período de eliminação (washout) e efeitos residuais (carry-over effects)

É importante introduzir os conceitos de período de eliminação e efeitos residuais num planejamento de estudo cruzado, pois a presença de efeitos residuais tem um grande impacto na inferência estatística de bioequivalência entre formulações.

O período de eliminação é definido como um intervalo de tempo suficientemente grande entre dois períodos de administração para que o efeito residual de uma formulação administrada num período seja eliminado até o próximo.

O experimento cruzado deve ser usado quando não existe efeito residual nos tratamentos. Se um fármaco tem uma meia vida longa ou se o intervalo entre os períodos de tratamento é muito curto, o efeito do mesmo pode persistir depois do fim de período de eliminação (efeito residual). Neste caso, é necessário distinguir a diferença entre o efeito do fármaco e os efeitos residuais. O efeito do fármaco é aquele observado durante o período no qual ele é administrado.

2.2 Descrição do planejamento

O estudo cruzado é um planejamento de blocos aleatorizados modificados nos quais cada bloco recebe mais de uma formulação de um mesmo fármaco em períodos diferentes. Um bloco pode ser um indivíduo ou um grupo de indivíduos. Os indivíduos em cada bloco recebem uma seqüência diferente de formulações. As vantagens em se utilizar esse planejamento para estudos de biodisponiblidade relativa/bioequivalência são:

·cada indivíduo serve como seu próprio controle, o que permite uma comparação do indivíduo com ele mesmo, para as diferentes formulações;

·a variabilidade inter-individual é removida da comparação entre formulações, o que torna o teste de diferença de tratamentos em geral mais poderoso;

·com uma aleatorização apropriada de indivíduos para a seqüência de administração das formulações, o planejamento produz as melhores estimativas não viciadas para diferença (ou razão) entre formulações.

2.3 Considerações de um delineamento básico

Recomenda-se que um delineamento básico para um estudo de biodisponibilidade in vivo deve considerar: ·questões científicas a serem respondidas;

·natureza do material de referência e a forma farmacêutica a ser testada;

·disponibilidade de métodos analíticos;

·considerações do benefício do teste em seres humanos.

Além disso, algumas considerações específicas para um estudo de biodisponiblidade relativa/bioequivalência são dadas a seguir.

2.3.1. Delineamento experimental

Para um estudo de biodisponibilidade relativa/bioequivalência (dose simples ou múltipla) deve ser adotado um delineamento do tipo cruzado, a não ser que um delineamento paralelo ou algum outro seja mais apropriado por razões científicas válidas. No caso de delineamento paralelo, cada indivíduo recebe ao acaso somente uma das formulações.

O planejamento adequado do experimento deve ter como objetivo minimizar a variabilidade que pode advir de várias fontes:

·variabilidade inter-individual.

·variabilidade intra-individual.

·efeito dos períodos, que pode ser causado por ação residual de tratamentos precedentes;

·erro experimental.

·variabilidade associada a tratamentos diferentes, como administração de produtos ou dosagens diferentes.

2.3.2. Aleatorização

Inferências estatísticas válidas são normalmente baseadas nas suposições de que os erros do modelo empregado são variáveis aleatórias independentemente distribuídas, o que pode ser assegurado através da aleatorização.

A forma de aleatorização é feita de acordo com o delineamento a ser utilizado no estudo.

2.3.3. Cronograma de coleta

2.3.4. Período de eliminação

2.3.5. Número de voluntários

O número de voluntários sadios deverá sempre assegurar poder estatístico suficiente para garantir a confiabilidade dos resultados do estudo de biodisponibilidade relativa/bioequivalência.

2.4 Tipos de desenho

ESTA SEÇÃO DESCREVE OS DESENHOS COMUMENTE UTILIZADOS NOS ESTUDOS DE BIODISPONIBILIDADE RELATIVA/BIOEQUIVALÊNCIA.

2.4.1. Delineamento cruzado para dois medicamentos (T = teste; R = referência)

a) Delineamento cruzado 2x2

É um delineamento convencional não replicado com duas formulações, dois períodos, duas seqüências, que pode ser representado como segue:

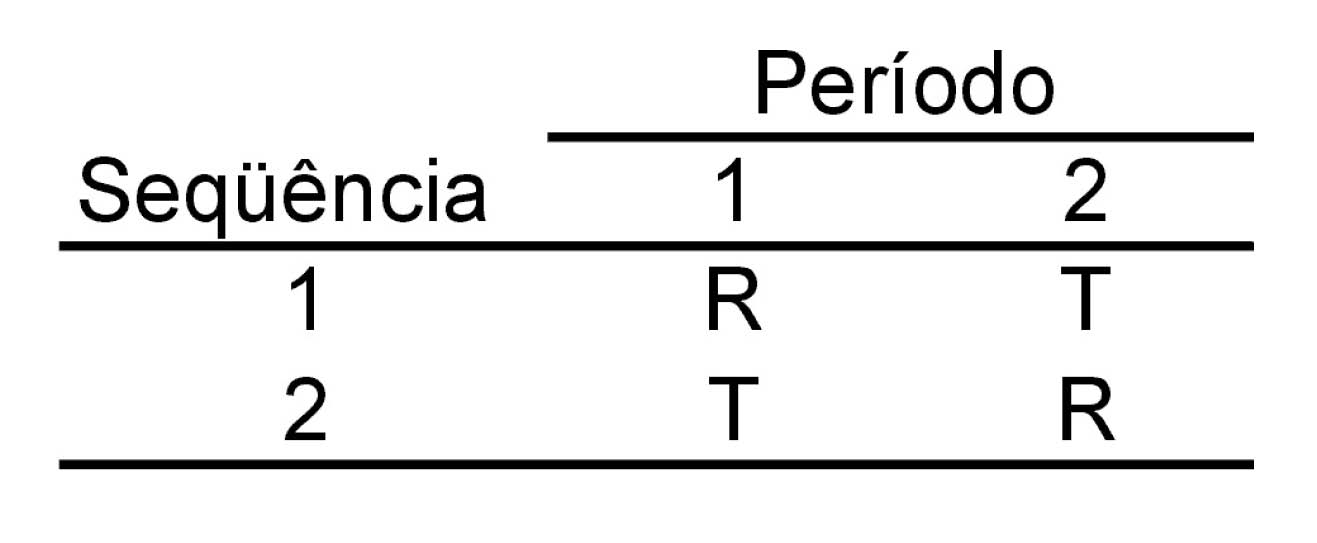
Cada indivíduo é aleatoriamente alocado para a seqüência RT ou TR em dois períodos. Isto é, indivíduos alocados na seqüência RT (TR) recebem formulação R (T) no primeiro período de administração e formulação T (R) no segundo. Os períodos são separados por um período de eliminação adequado.

Aleatorização para um estudo cruzado 2x2 pode ser feita através de tabelas de números aleatórios ou procedimentos de aleatorização implementados em softwares estatísticos.

b) Delineamento cruzado replicado

Este delineamento é recomendado para estudos de biodisponibilidade relativa/bioequivalência de produtos com fármacos de alta variabilidade (coeficiente de variação intra-individual ≥ 30%), incluindo aqueles que são de liberação imediata, liberação modificada e outros produtos de administração oral.

Para este delineamento os mesmos lotes das formulações teste e referência devem ser usados para a administração replicada.
Os períodos devem ser suficientemente espaçados para garantir a inexistência do efeito residual.

Os desenhos cruzados replicados mais comumente usados para comparar duas formulações são:

I. Delineamento com quatro seqüências e dois períodos (delineamento de Balaam):

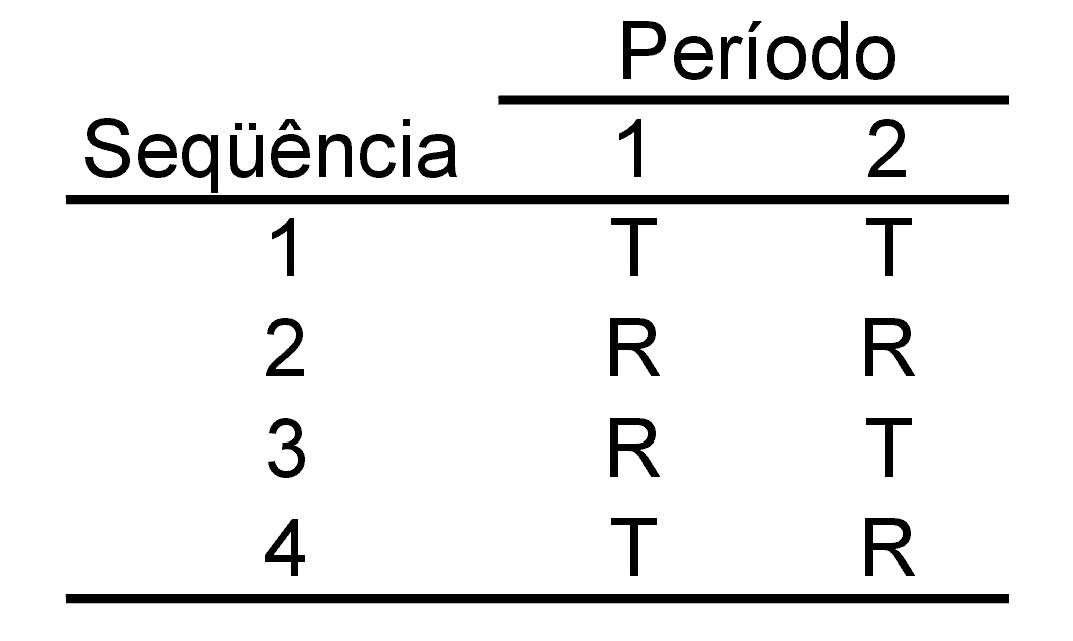
II. Delineamento com duas seqüências e quatro períodos:

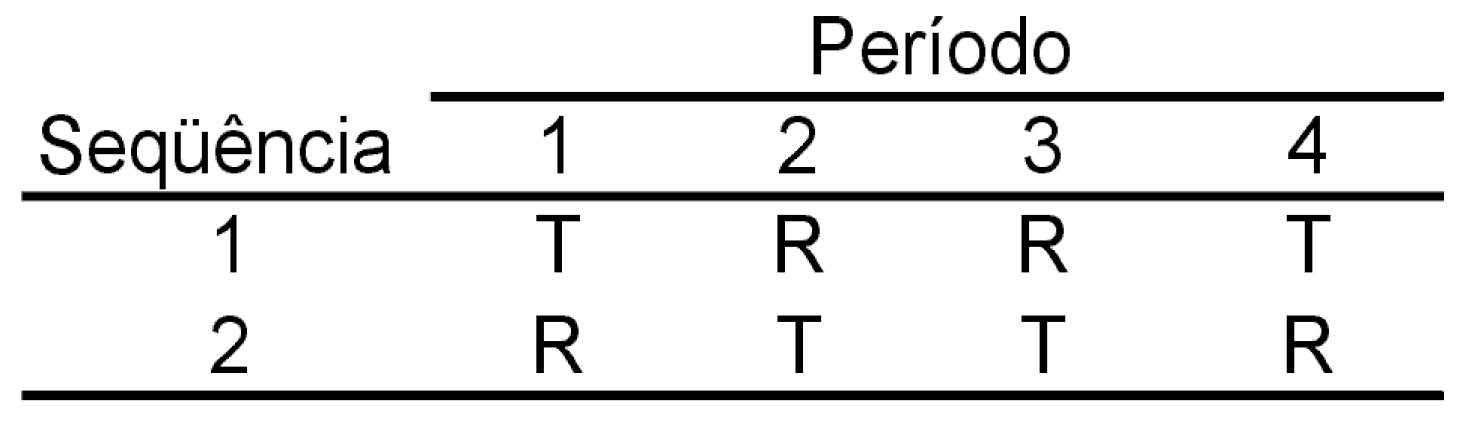
III. Delineamento com quatro seqüências e quatro períodos:

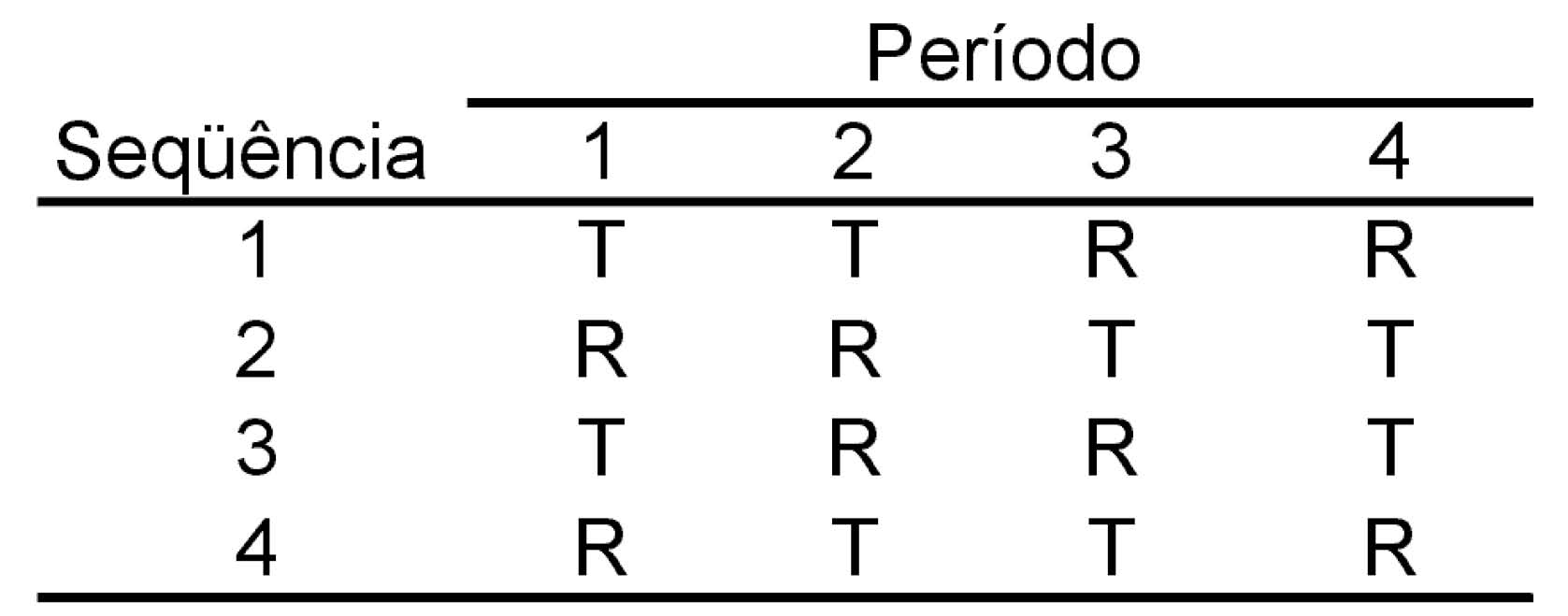
IV. Delineamento com duas seqüências e três períodos:

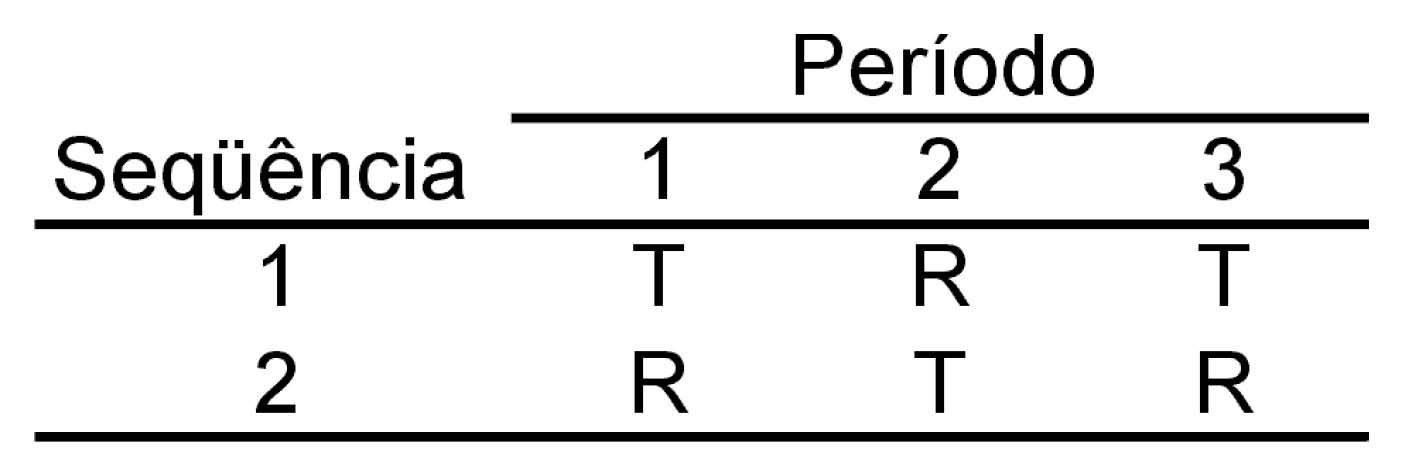
Ou

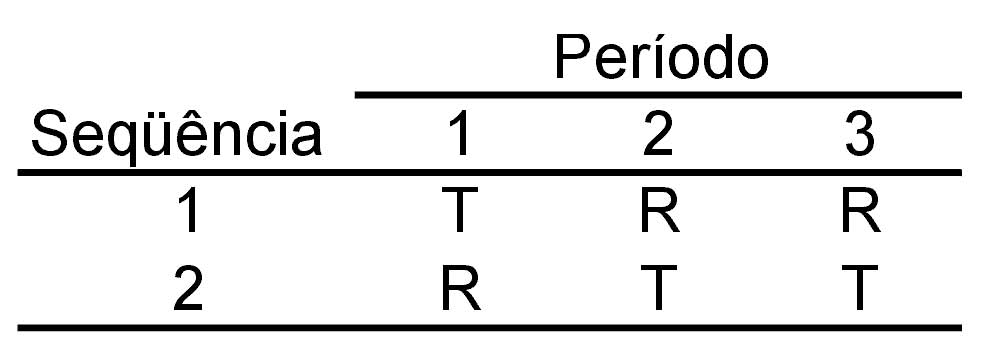
Um número maior de voluntários é recomendado para o delineamento de três períodos, comparado com o delineamento de quatro períodos, para poder alcançar o mesmo poder estatístico para o teste.

c) Delineamento cruzado para três medicamentos (delineamento de Williams com T1 = teste 1, T2 = teste 2, R = referência)

Para comparar três formulações de um fármaco, existem três possíveis pares de comparações: formulação 1 versus formulação 2, formulação 1 versus formulação 3 e formulação 2 versus formulação 3. Quando o número de formulações a serem comparadas é grande, mais seqüências e conseqüentemente mais indivíduos serão necessários, o que pode ser inviável. Um delineamento de uso prático proposto por Williams (1949) possui propriedades de balanceamento e requer poucas seqüências e períodos. Um delineamento é dito balanceado se satisfaz as seguintes condições:

•cada medicamento é aplicado somente uma vez em cada voluntário;

•em cada período, o número de voluntários que recebemcada medicamento tem que ser igual;

•o número de voluntários que recebem o medicamento i em algum período seguido pelo medicamento j no período seguinte é o mesmo para todo i≠j.

Um delineamento de Williams é ilustrado como segue:

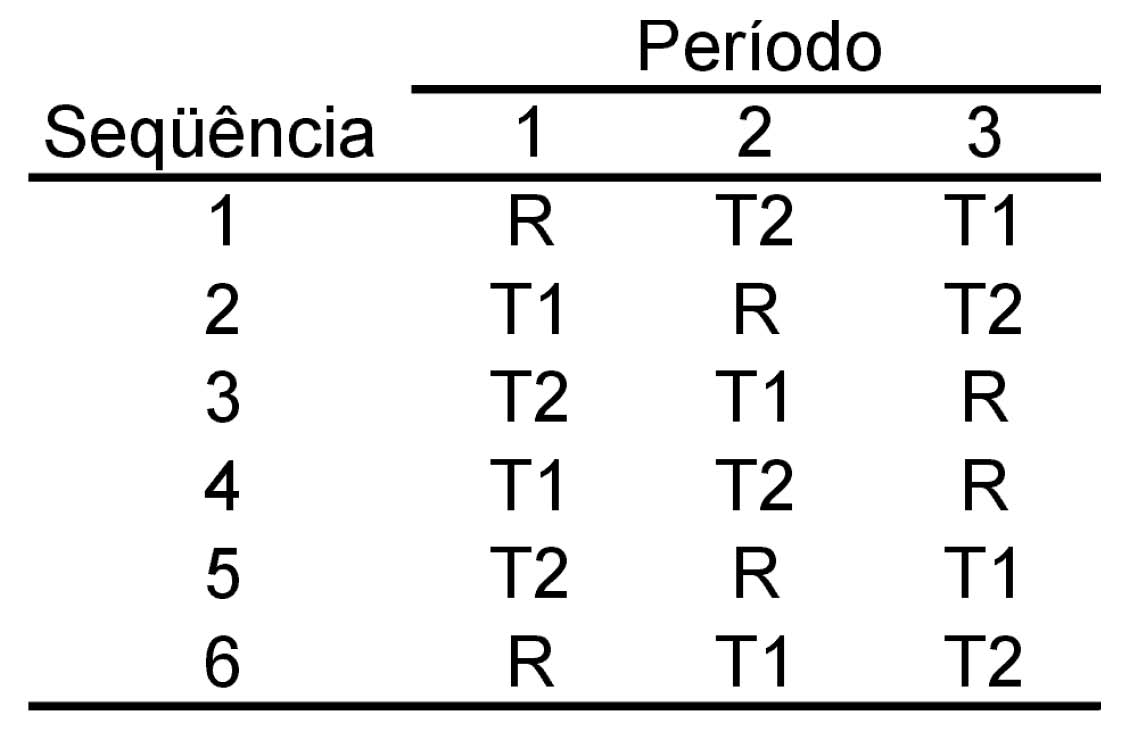
d) Delineamento cruzado para quatro medicamentos (delineamento de Williams):

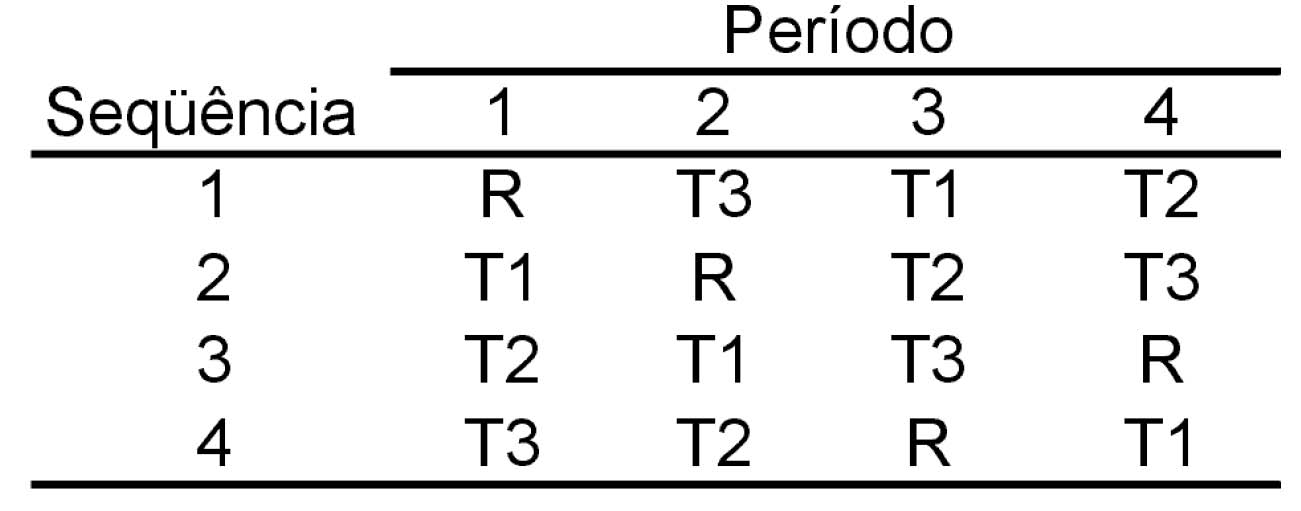
2.5 Seleção do delineamento experimental

Selecionar um delineamento apropriado ao planejar um estudo de biodisponibilidade relativa/ bioequivalência é uma questão importante. A resposta dessa questão depende de vários fatores, tais como:

·número de formulações a serem comparadas;

·características do fármaco e sua biodisponibilidade;

·objetivo do estudo; ·variabilidade inter e intra individuais;

·duração do estudo e número de períodos empregados; ·custo de adição de um voluntário relativo à adição de um período;

·taxa de desistência (dropout).

A análise dos dados, a interpretação dos resultados e a determinação de bioequivalência entre as formulações, dependem diretamente do delineamento selecionado. Portanto, todos os fatores citados acima devem ser cuidadosamente avaliados para que um delineamento apropriado seja escolhido.

3 Análise Estatística

3.1 Transformação logarítmica

3.1.1 Procedimento geral

Este guia recomenda que os valores dos parâmetros (ASC e Cmax) sejam transformados usando logaritmo natural ou logaritmo comum em base 10. A escolha de logaritmo natural ou comum deve ser consistente e deve ser especificada no relatório de estudo.

A limitação do tamanho de amostra utilizada num estudo típico de biodisponibilidade relativa/bioequivalência impede uma determinação confiável de distribuição do conjunto de dados. Não é recomendável testar normalidade de distribuição de erros depois de transformação logarítmica, nem se deve utilizar normalidade de distribuição de erros como uma razão para fazer análise estatística nas escalas originais. Justificativas devem ser apresentadas no caso em que se considera que é melhor realizar a análise estatística nas escalas originais do que nas escalas logarítmicas.

3.1.2 Justificativas para utilização de transformação logarítmica

a) Justificativa em relação ao tratamento de dados

Em geral, uma comparação preliminar de interesse num estudo de biodisponibilidade relativa/bioequivalência é a utilização da razão ao invés da diferença, entre as médias dos parâmetros farmacocinéticos (ASC e Cmax) dos dados do produto teste e de referência. Usando transformação logarítmica, o modelo linear generalizado empregado na análise de dados permite fazer inferências estatísticas sobre a diferença entre duas médias na escala logarítmica, as quais podem ser re-transformadas em inferências estatísticas sobre a razão das duas médias na escala original (Schuirmann, 1989).

b) Justificativa em relação a farmacocinética

Westlake (1973, 1988) observou que um modelo multiplicativo é adequado para medidas farmacocinéticas (ASC e Cmax) num estudo de biodisponibilidade relativa/bioequivalência. Assumindo que a eliminação do fármaco é de primeira ordem e somente ocorre a partir do compartimento central, a seguinte equação é obtida após uma administração extravascular (oral):

ASC0-∞ = F.D/CL = F.D/(Vd.Ke),

onde: F é a fração absorvida, D é a dose administrada, e F.D é a quantidade do fármaco absorvido. CL é o "clearance" de um dado voluntário, o qual é o produto do volume de distribuição aparente (Vd) e da constante de velocidade de eliminação (Ke). Portanto, o uso de ASC como uma medida da quantidade de medicamento absorvido envolve um termo multiplicativo (CL), o qual pode ser considerado como uma função do voluntário. Por essa razão, Westlake mostra que o efeito de voluntário não é aditivo se os dados são analisados na escala original.

A transformação logarítmica da ASC resulta num tratamento aditivo:

log ASC0-∞ = log F + log D - log V - log Ke.

Argumentos semelhantes foram dados para Cmax

3.2 Análise dos dados

Os métodos paramétricos de modelos lineares generalizados são recomendáveis para a análise de medidas farmacocinéticas transformadas em logaritmo num estudo de biodisponibilidade relativa/bioequivalência. Uma análise de variância (ANOVA) deve ser empregada nos parâmetros farmacocinéticos ASC e Cmax usando modelos lineares generalizados. Modelos estatísticos apropriados de acordo com o desenho escolhido no estudo devem ser empregados. Por exemplo, para um estudo convencional do tipo cruzado 2x2, o modelo estatístico normalmente inclui fatores de seqüência, voluntário dentro de seqüência, período e tratamento. O resultado deve ser representado como a seguir (tabela ANOVA):

Fonte	Grau de liberdade	Quadrado médio	Estatística F	Valor de P
Seqüência	1	(1)	Fr=(1)/(2)
voluntário (seqüência)	N-2	(2)
Período	1	(3)	Fp=(3)/(5)
Tratamento	1	(4)	Ft=(4)/(5)
Residual	N-2	(5)

Os efeitos de seqüência, de período e de tratamento devem ser testados usando estatísticas Fr, Fp e Ft indicadas na tabela ANOVA, respectivamente. Deve-se notar que a igualdade entre tratamentos (inexistência de efeito de tratamento) não implica na bioequivalência entre formulações. A construção do intervalo de confiança de 90% para a diferença das médias deve ser baseada nas médias de mínimos quadrados dos dados transformados em logarítmicos e no quadrado médio residual dessa ANOVA. Os antilogaritmos dos limites de confiança obtidos constituem o intervalo de confiança de 90% para a razão das médias geométricas entre os produtos teste e referência. A conclusão de bioequivalência média é alcançada quando este intervalo de confiança está compreendido entre 80 e 125%. Este método é equivalente ao procedimento de dois testes unicaudais correspondentes à hipótese nula de bioinequivalêcia, com nível de significância de 5%.

4. Efeito de seqüência

A presença de efeitos seqüênciais (residuais) no estudo deve ser justificada. Para um estudo cruzado 2x2, a presença de efeitos seqüenciais pode ser aceita se alguns critérios forem observados:

I) é um estudo de dose única;

II) estudo envolve somente voluntários sadios;

III) o fármaco não é uma substância endógena;

IV) um período de eliminação adequado foi estabelecido e as amostras de pré-dosagem não apresentam qualquer nível de fármaco detectável em todos os voluntários;

V) o estudo satisfaz todos os critérios científicos e estatísticos (por exemplo, protocolo, validação, dados de concentração, análise estatística, intervalo de confiança). Sob outras circunstâncias, o estudo deve ser refeito.

5. Considerações de outliers

NO ESTUDO DE BIODISPONIBILIDADE RELATIVA/BIOEQUIVALÊNCIA COM DESENHO CRUZADO, OS PONTOS DISCREPANTES SÃO DEFINIDOS COMO AQUELES EM QUE ALGUNS VOLUNTÁRIOS (OUTLIERS) DIFEREM NOTAVELMENTE DOS DEMAIS VOLUNTÁRIOS DO ESTUDO COMPARANDO PRODUTO TESTE E REFERÊNCIA NO PRÓPRIO VOLUNTÁRIO. A EXISTÊNCIA DE UM OUTLIER SEM VIOLAÇÃO DO PROTOCOLO PODE INDICAR UMA DAS SEGUINTES SITUAÇÕES:

A) FALHA DO PRODUTO: NESTE CASO, UMA RESPOSTA ANORMAL PODE ESTAR PRESENTE TANTO PARA PRODUTO TESTE QUANTO PARA PRODUTO REFERÊNCIA;

B) SUBPOPULAÇÃO: ISTO PODE OCORRER QUANDO UM INDIVÍDUO REPRESENTA UMA POPULAÇÃO, NA QUAL A BIODISPONIBILIDADE DE DOIS PRODUTOS É NOTAVELMENTE DIFERENTE DA MAIORIA DA POPULAÇÃO.

Devido esses fatos, em geral, a exclusão de outliers não é recomendável, principalmente para desenhos não replicados.

6. O poder do teste e tamanho da amostra

O poder do teste de um estudo de biodisponibilidade relativa/bioequivalência é definido como a probabilidade de aceitar a bioequivalência entre produto teste e referência corretamente. Durante a etapa de planejamento, uma das questões mais importantes é quantos voluntários são necessários para obter um poder desejado (por exemplo, 80%) estabelecendo bioequivalência entre duas formulações dentro dos limites clinicamente importantes (por exemplo, 20% da média do referência). Para responder essa questão, a metodologia comumente utilizada é escolher um tamanho de amostra apropriado através do cálculo da função do poder do teste baseado numa estimativa de coeficiente de variação intra-individual obtida através da literatura ou de um estudo piloto.

Na literatura, existem diversas maneiras para determinar o tamanho da amostra. Neste guia, é apresentada uma fórmula aproximada (Chow & Liu) para calcular o tamanho da amostra de um desenho cruzado 2x2 baseada na função de poder do teste por hipótese de intervalo de Schuirmann. A determinação do tamanho da amostra para outros tipos de desenho deve ser feita de maneira análoga.

Define-se a medida θ = μT - μR, ou seja, θ mede a verdadeira diferença entre as médias do produto teste e referência. Num estudo de bioequivalência média, considerando a regra de 20% com Δ=0,2 μR, para alcançar um poder de (1-β) com nível de significância α, o tamanho da amostra para cada seqüência é:

a) no caso de θ = 0,

n ≥ [t(α, 2n-2) + t(β/2, 2n-2)]2 (CV/20)2;

b) no caso de θ ≠ 0,

n ≥ [t(α, 2n-2) + t(β, 2n-2)]2 [CV/(20-η)]2,

onde η = 100 x θ/μR = 100 x (μT - μR)/ μR.

Nas duas fórmulas apresentadas acima, CV representa o coeficiente de variação intra-individual e t(a,b) representa o valor crítico
da distribuição t de Student, ao nível de significância a com b graus de liberdade.

O total de voluntários necessários para um desenho cruzado 2x2 é:

N = 2n

Como o grau de liberdade (2n-2) apresentado na fórmula é desconhecido, um procedimento iterativo é necessário para obtenção do valor de n. Para ilustrar este procedimento, apresenta-se o seguinte exemplo.

Exemplo: Para conduzir um estudo de bioequivalência média utilizando desenho cruzado 2x2 e a regra de 20% de diferença entre duas formulações, deseja-se determinar o número de voluntários necessários para obter um poder de 80% detectando uma diferença de 20% entre duas formulações. Supondo que o CV neste exemplo é 20%.

Em primeiro lugar, considera-se o caso onde θ = 0,

I) começando com um chute inicial: n=12;

II) então, temos o grau de liberdade 2n-2=22;

III) utiliza-se α = 0,05 e β = 0,2, temos

t(0,05, 22) = 1,717 e t(0,1, 22) =1,321;

IV) n ≥ (1,717 + 1,321)2 (20/20)2 ≈ 9,2;

V) agora use-se n = 10 como um valor inicial para próxima iteração;

VI) 2n-2 = 18, t(0,05, 18) = 1,734 e t (0,10, 18) = 1,330;

VII) n ≥ (1,734 + 1,330)2 (20/20)2 ≈ 9,4 ;

VIII) como essas duas iterações resultaram uma resposta similar de 10 voluntários para cada seqüência, um total de 20 voluntários deve ser necessário no sentido de obter um poder 80% para detectar uma diferença de 20% entre duas formulações para o caso de θ = 0.

Agora considera-se o caso de θ = 0,05 μR,

I) começando com um chute inicial: n=14;

II) então, temos o grau de liberdade 2n-2=26;

III) utiliza-se α = 0,05 e β = 0,2, temos

t(0,05, 26) = 1,706 e t(0,2, 26) = 0,856;

IV) n ≥ (1,706 + 0,856)2 [20/(20-5)]2 ≈ 11,66;

V) para próxima iteração, utiliza-se n = 12 como um valor inicial;

VI) 2n-2 = 22, t(0,05, 22) = 1,717 e t (0,20, 22) = 0,858;

VII) n ≥ (1,717 + 0,858)2 [20/(20-5)]2 ≈ 11,79;

VIII) portanto, um total de 24 voluntários deve ser necessário no sentido de obter um poder 80% para detectar uma diferença de 20% entre duas formulações para o caso de θ = 0,05 μR.

A tabela a seguir apresenta o total de tamanho da amostra necessário para alcançar um poder desejado para um desenho cruzado 2x2 de diversas combinações entre θ e CV.

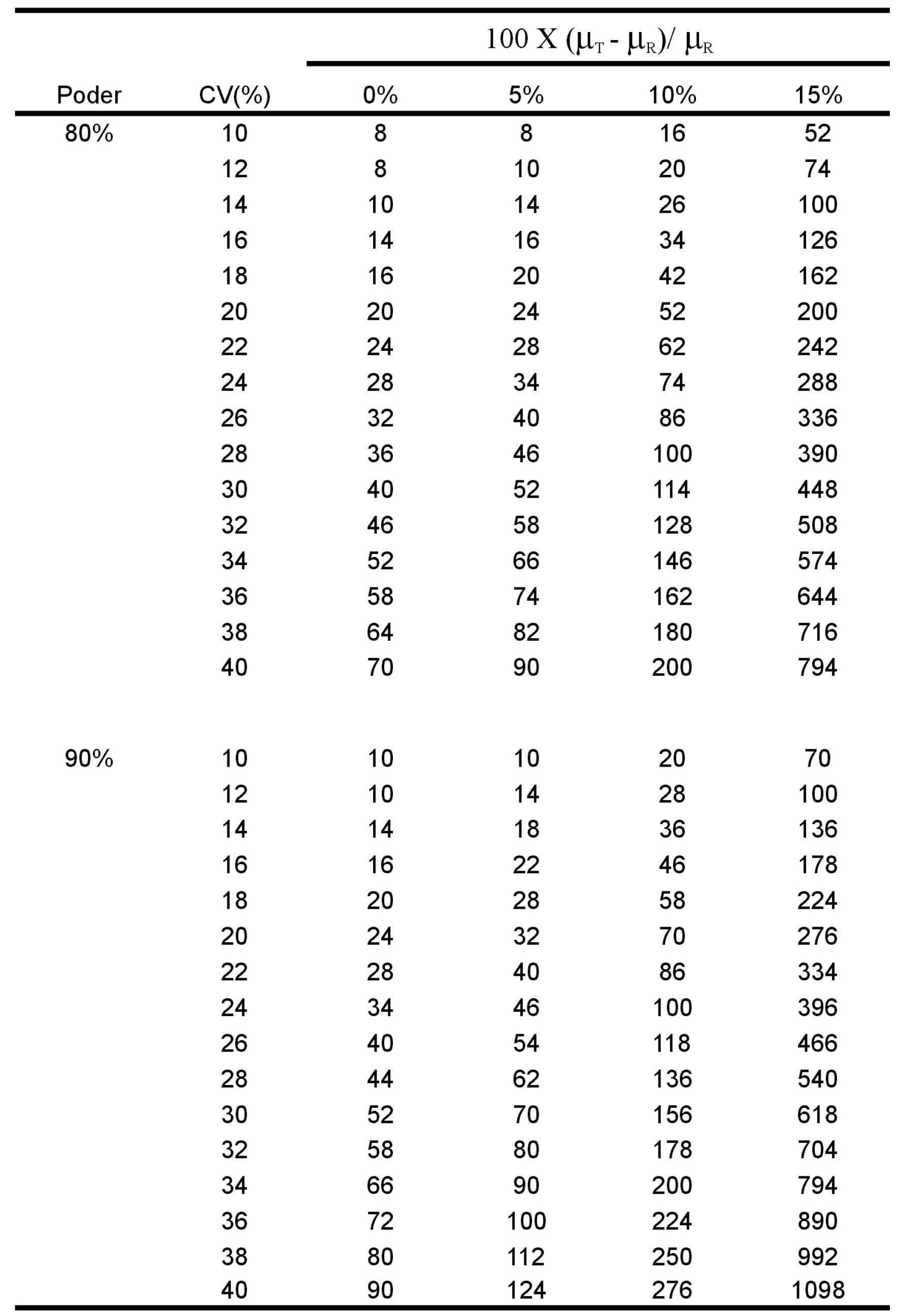
7. Outras considerações

O critério da bioequivalência média é recomendado para uma comparação entre as medidas farmacocinéticas de interesse na maioria dos estudos de biodisponibilidade relativa/bioequivalência. Entretanto, na literatura, existem os critérios de bioequivalência individual e populacional que também podem ser muito úteis em algumas circunstâncias.

A bioequivalência média focaliza-se somente na comparação das médias populacionais de medidas farmacocinéticas de interesse e não nas variâncias dessas medidas. Este método não leva em consideração a variância associada à interação entre indivíduos e formulações, ou seja, a variação entre as médias dos produtos teste e referência devido às diferenças existentes entre os indivíduos. Já os critérios de bioequivalência individual e populacional incluem as comparações além das médias, as respectivas variâncias associadas às medidas farmacocinéticas de estudo. O critério da bioequivalência populacional avalia a variabilidade total das medidas de interesse. O critério de bioequivalência individual engloba a variabilidade intra-individual dos produtos teste e referência, bem como as interações entre indivíduos e formulações.

Hauck & Anderson (1992) apresentam considerações e comparações dos três tipos de bioequivalência, bem como as indicações para a construção dos intervalos de confiança.

8. Referências Bibliográficas

Chow, S.C.; Liu, J-P. Design and Analysis of Bioavailability and Bioequivalence Studies. New York: Marcel Dekker. 2000

Diletti, E.; Hauschke, D.;Steinijans, V.W. Sample Size Determination for Bioequivalence Assessment By Means of Confidence Intervals, Int. J. Clin. Pharmacol. Therap., 29:1-8. 1991

Guidence for industry - Statistical Approaches to Establishing Bioequivalence

U.S. Department of Health and Human Services; FDA - CDER, January 2001.

Hauck, W.W.; Anderson, S. Types of Bioequivalence and Related Statistical Considerations. Int. J. Clin. Pharmacol. Therap., 30:181-7, 1992.

Liu, J-P. Use of the Repeated Crossover Designs in Assessing Bioequivalence, Stat. Med., 14:1067-78, 1995.

Schuirmann, D.J. Treatment of Bioequivalence Data: Log Transformation, in Proceedings of Bio-International' 89 - Issues in the Evaluation of Bioavailability Data, Toronto, Canada, October 1-4, 159-61, 1989.

Westlake, W.J. The Design and Analysis of Comparative Blood-Level Trials, in Current Concepts in the Pharmaceutical Sciences, Dosage Form Design and Bioavailability (J.Swarbrick, ed.), Lea and Febiger, 149-79, 1973.

Westlake, W.J. Bioavailability and Bioequivalence of Pharmaceutical Formulations, in Biopharmaceutical Statistics for Drug Development (K.E.Peace, ed.), Marcel Dekker, Inc., 329-52, 1988.